Garis boleh dijumpai di mana sahaja dalam matematik, sama ada anda mengambil Algebra 1, Geometri, atau Algebra 2. Sekiranya anda mengetahui cara mencari kecerunan garis, banyak perkara akan menjadi jelas, misalnya jika kedua-dua garis itu selari atau tegak lurus, bersilang, dan banyak konsep lain. Mencari kecerunan garis sebenarnya sangat mudah. Teruskan membaca untuk beberapa langkah mudah yang boleh anda gunakan untuk belajar bagaimana mencari kecerunan garis.
Langkah
Kaedah 1 dari 2: Formula Kecerunan
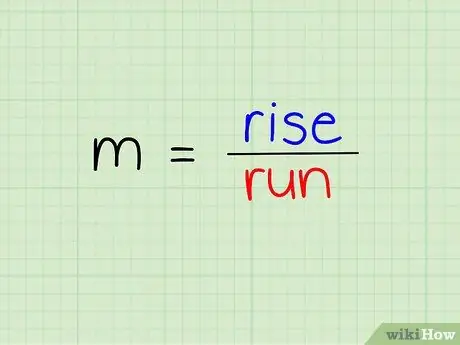
Langkah 1. Fahami formula kecerunan
Kecerunan ditakrifkan sebagai menegak dibahagi dengan mendatar.
Kaedah 2 dari 2: Mencari Kecerunan
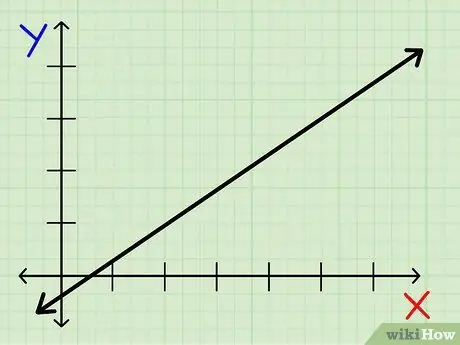
Langkah 1. Cari garis yang anda inginkan untuk mencari kecerunan
Pastikan garis lurus. Anda tidak dapat mencari kecerunan garis yang tidak lurus.
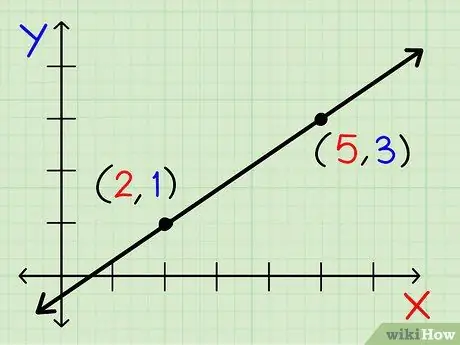
Langkah 2. Pilih dua koordinat yang dilalui oleh garis
Koordinat adalah titik x dan y yang ditulis (x, y). Tidak kira titik mana yang anda pilih, asalkan poinnya berbeza dan terletak pada baris yang sama.
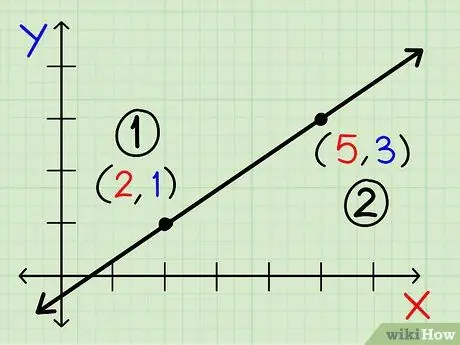
Langkah 3. Pilih titik koordinat yang dominan dalam persamaan anda
Tidak kira titik mana yang anda pilih, selagi nilainya selalu sama semasa pengiraan. Koordinat dominan ialah x 1 dan y 1. Koordinat yang lain ialah x 2 dan y 2.
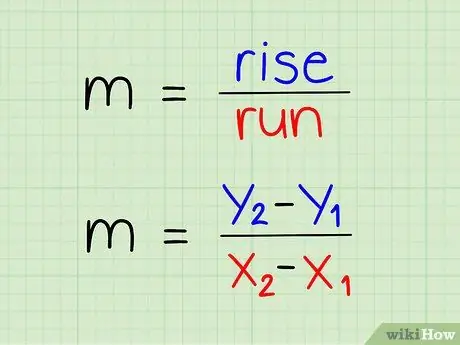
Langkah 4. Tuliskan persamaan anda dengan koordinat-y di atas dan koordinat-x di bawah
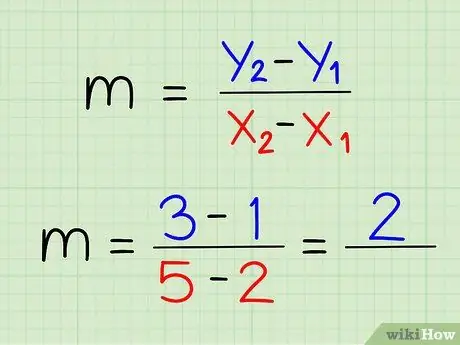
Langkah 5. Kurangkan dua koordinat y antara satu sama lain
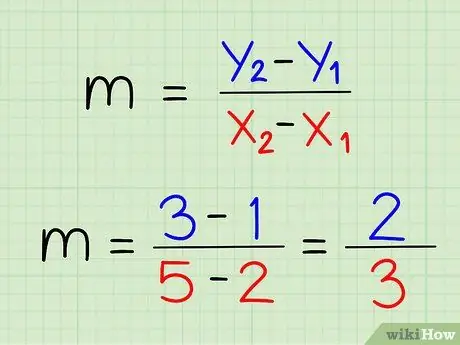
Langkah 6. Kurangkan koordinat dua x antara satu sama lain
Langkah 7. Bahagikan hasil penolakan koordinat-y dengan hasil penolakan koordinat-x
Permudahkan nombor jika boleh dipermudahkan.
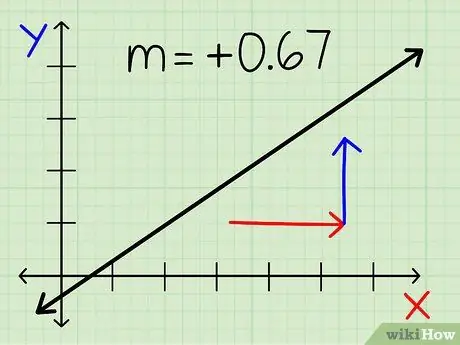
Langkah 8. Semak semula untuk mengetahui sama ada jawapan anda masuk akal
- Garis yang bergerak dari kiri ke kanan selalu positif, walaupun merupakan pecahan.
- Garis yang turun dari kiri ke kanan selalu negatif, walaupun pecahan.
Contohnya
- Dikenali: Talian AB.
- Koordinat: A - (-2, 0) B - (0, -2)
- (y2-y1): -2-0 = -2; Tegak = -2
- (x2-x1): 0 - (- 2) = 2; Mendatar = 2
-
Kecerunan Garisan AB = (Vertical / Horizontal) = -1.
Petua
- Sekiranya anda telah memilih koordinat titik dominan anda, jangan menukarnya untuk koordinat lain atau jawapan anda akan salah.
- Anda akan menjumpai m dalam Formula Garis, iaitu: y = mx + b, di mana y adalah koordinat-y bagi mana-mana titik, m adalah kecerunan, x adalah koordinat-x yang sesuai dengan koordinat-y pada titik mana pun, dan b ialah pintasan-y.
- Anda juga boleh melihat buku teks sekolah anda atau bertanya kepada guru anda.
