- Pengarang Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:14.
- Diubah suai terakhir 2025-01-23 12:42.
Semua orang boleh belajar Matematik sama ada mereka sudah berada di peringkat yang lebih tinggi di sekolah atau yang hanya ingin mengasah asasnya lagi. Setelah membincangkan bagaimana menjadi pelajar yang baik dalam Matematik, artikel ini akan mengajar anda kemajuan asas matematik dan akan memberi anda elemen asas yang perlu anda pelajari dalam setiap latihan. Kemudian, artikel ini akan membincangkan asas-asas belajar aritmetik, yang akan membantu anak-anak sekolah rendah dan semua orang yang ingin mempelajari asas-asas bidang sains ini.
Langkah
Bahagian 1 dari 6: Kunci untuk Menjadi Pelajar Matematik yang Baik

Langkah 1. Muncul di kelas
Apabila anda ketinggalan kelas, anda harus mempelajari konsep dari rakan sekelas atau dari buku teks anda. Anda tidak akan mendapat ringkasan teks daripada rakan seperti yang anda dapatkan dari guru anda.
- Datang ke kelas tepat pada waktunya. Sebagai gantinya, tiba lebih awal dan buka buku nota anda di tempat yang betul, buka buku teks anda dan keluarkan kalkulator anda supaya anda bersedia memulakannya apabila guru anda sudah bersedia untuk mengajar.
- Curang jika anda sakit. Sekiranya anda betul-betul ketinggalan kelas, minta rakan sekelas anda untuk mengetahui apa yang dibincangkan oleh guru dan apa kerja rumah yang diberikan.

Langkah 2. Bekerja dengan guru anda
Sekiranya guru anda menyelesaikan masalah di hadapan kelas, bekerjasama dengan guru dengan menyelesaikan masalah di buku nota anda.
- Pastikan nota anda jelas dan senang dibaca. Jangan hanya menulis soalan. Tulis juga apa sahaja yang dikatakan oleh guru yang dapat meningkatkan pemahaman anda mengenai konsep yang dijelaskan.
- Lengkapkan contoh soalan yang diberikan oleh guru anda. Semasa guru berjalan di sekitar kelas semasa anda bekerja, jawab soalan yang diajukan.
- Ikut serta semasa guru menyelesaikan masalah. Jangan tunggu guru memanggil anda. Tawarkan untuk menjawab apabila anda mengetahui jawapannya, dan angkat tangan untuk mengemukakan soalan sekiranya anda tidak yakin dengan bahan yang diajar.

Langkah 3. Lakukan kerja rumah anda pada hari yang sama dengan kerja rumah anda diberikan
Sekiranya anda membuat kerja rumah pada hari yang sama, konsepnya masih segar di fikiran anda. Kadang kala, menyelesaikan kerja rumah anda pada hari yang sama tidak mungkin. Pastikan kerja rumah anda selesai sebelum masuk ke kelas.

Langkah 4. Bekerja di luar kelas jika anda memerlukan pertolongan
Lawati guru anda semasa rehat atau waktu pejabat.
- Sekiranya anda mempunyai Pusat Matematik di sekolah anda, ketahui waktu buka dan minta pertolongan.
- Sertai kumpulan belajar. Kumpulan belajar yang baik umumnya terdiri daripada 4 atau 5 orang dengan tahap kemampuan yang berbeza. Sekiranya anda pelajar "C" dalam Matematik, sertai kumpulan 2 atau 3 pelajar dengan gred "A" atau "B" supaya anda dapat meningkatkan kemahiran anda. Elakkan menyertai kumpulan pelajar yang nilainya lebih rendah daripada anda.
Bahagian 2 dari 6: Pembelajaran Matematik di Sekolah

Langkah 1. Mulakan dengan aritmetik
Di kebanyakan sekolah, pelajar belajar aritmetik di sekolah rendah. Aritmetik merangkumi asas penambahan, pengurangan, pendaraban dan pembahagian.
- Lakukan soalan latihan. Melakukan masalah aritmetik berulang kali adalah kaedah terbaik untuk menghafal asas dengan betul. Cari perisian yang dapat memberi anda pelbagai masalah Matematik yang berbeza untuk dikendalikan. Juga, cari masalah dengan jangka masa untuk meningkatkan kelajuan anda.
- Anda juga dapat menemui masalah aritmetik dalam talian, dan anda boleh memuat turun aplikasi aritmetik ke peranti mudah alih anda.

Langkah 2. Teruskan dengan pra-algebra
Latihan ini akan memberi anda elemen asas yang anda perlukan untuk menyelesaikan masalah aljabar di kemudian hari.
- Ketahui mengenai pecahan dan perpuluhan. Anda akan belajar menambah, mengurangkan, mengalikan, dan membahagi pecahan dan perpuluhan. Mengenai pecahan, anda akan belajar cara mengurangkan pecahan dan menterjemahkan nombor gabungan. Mengenai perpuluhan, anda akan memahami nilai tempat, dan anda akan dapat menggunakan perpuluhan dalam masalah cerita.
- Ketahui mengenai nisbah, perkadaran dan peratusan. Konsep-konsep ini akan membantu anda belajar membuat perbandingan.
- Perkenalkan diri dengan asas geometri. Anda akan mempelajari bentuk dan konsep 3D. Anda juga akan mempelajari konsep seperti luas, perimeter, isipadu dan luas permukaan, serta maklumat mengenai garis dan sudut selari dan tegak lurus.
- Fahami beberapa statistik asas. Dalam pra-aljabar, pengenalan anda pada statistik umumnya merangkumi visual seperti grafik, carta sebaran, carta plot setem dan histogram.
- Ketahui asas algebra. Ini merangkumi konsep seperti menyelesaikan persamaan mudah yang mengandungi pemboleh ubah, belajar mengenai sifat seperti harta pengagihan, melukis persamaan mudah, dan menyelesaikan ketaksamaan.
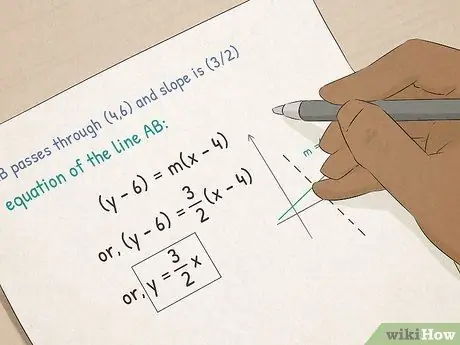
Langkah 3. Maju ke Algebra I
Pada tahun pertama aljabar, anda akan belajar mengenai simbol asas yang terdapat dalam aljabar. Anda juga akan belajar untuk:
- Selesaikan persamaan dan ketaksamaan yang mengandungi pemboleh ubah. Anda akan belajar bagaimana menyelesaikan masalah ini di atas kertas dan bagaimana menyelesaikannya dengan gambar.
- Selesaikan masalah cerita. Anda akan terkejut berapa banyak masalah sehari-hari yang akan anda hadapi pada masa akan datang yang memerlukan kemampuan menyelesaikan masalah cerita algebra. Contohnya, anda akan menggunakan aljabar untuk mengetahui kadar faedah yang anda perolehi di akaun bank atau pelaburan anda. Anda juga boleh menggunakan aljabar untuk mengetahui berapa lama perjalanan anda perlu dilakukan berdasarkan kelajuan kereta anda.
- Bekerja dengan eksponen. Apabila anda mula menyelesaikan persamaan polinomial (ungkapan yang mengandungi nombor dan pemboleh ubah), anda akan memahami cara menggunakan eksponen. Ini mungkin merangkumi latihan dengan notasi saintifik. Setelah anda menguasai eksponen, anda dapat belajar menambahkan, mengurangkan, membiak dan membahagi ungkapan polinomial.
- Selesaikan masalah punca kuasa dua dan kuasa dua. Semasa anda menguasai topik ini, anda akan dapat menghafal kotak dengan nombor yang banyak. Anda juga akan dapat bekerja dengan persamaan yang mempunyai punca kuasa dua.
- Memahami fungsi dan grafik. Dalam aljabar, anda akan belajar mengenai persamaan grafik. Anda akan belajar bagaimana mengira cerun garis, bagaimana meletakkan persamaan dalam bentuk titik-cerun, dan bagaimana mengira irisan garis x-dan-y menggunakan bentuk pintasan cerun.
- Ketahui sistem persamaan. Kadang kala, anda diberi 2 persamaan yang berbeza dengan pemboleh ubah x dan y, dan anda harus menyelesaikan x atau y untuk kedua-dua persamaan tersebut. Nasib baik, anda akan belajar banyak helah untuk menyelesaikan persamaan ini termasuk membuat grafik, penggantian dan penambahan.

Langkah 4. Mengkaji geometri
Dalam geometri, anda akan belajar mengenai sifat garis, segmen, sudut dan bentuk.
- Anda akan menghafal sejumlah teorema dan keputusan yang akan membantu anda memahami peraturan geometri.
- Anda akan belajar bagaimana mengira luas bulatan, bagaimana menggunakan teorema Pythagoras dan bagaimana mencari hubungan antara sudut dan sisi segitiga khas.
- Anda akan melihat banyak soalan geometri dalam ujian standard masa depan seperti SAT, ACT dan GRE.
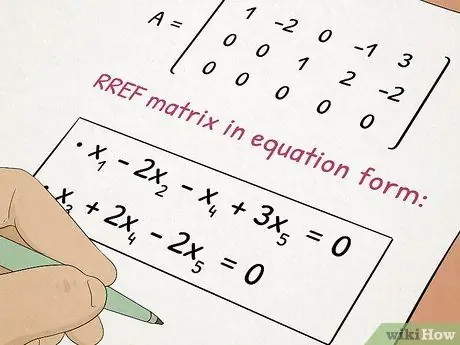
Langkah 5. Ikuti kelas Algebra II
Algebra II membina konsep yang telah anda pelajari di Algebra I sambil menambah topik yang kompleks seperti persamaan kuadratik dan matriks.
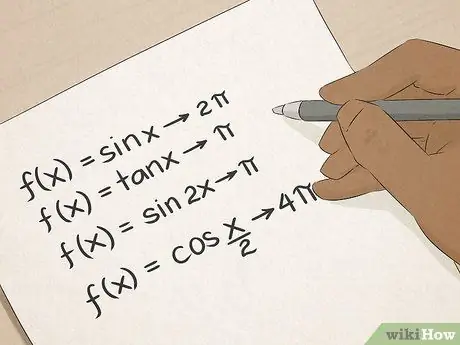
Langkah 6. Master trigonometri
Anda tahu istilah trigonometri: sinus, kosinus, tangen, dan sebagainya. Trigonometri akan mengajar anda banyak cara praktikal untuk mengira sudut dan panjang garis, dan kemahiran ini akan sangat berharga bagi orang yang bekerja dalam pembinaan, seni bina, kejuruteraan atau tinjauan.
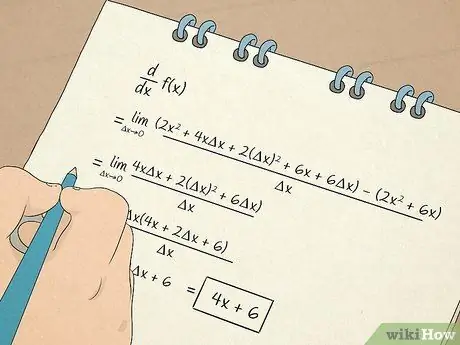
Langkah 7. Lakukan pengiraan kalkulus
Kalkulus mungkin terdengar menakutkan, tetapi ia adalah alat yang baik untuk memahami tingkah laku nombor atau dunia di sekeliling anda.
- Kalkulus akan mengajar anda fungsi dan had. Anda akan melihat bilangan tingkah laku fungsi berguna termasuk fungsi e ^ x dan logaritmik.
- Anda juga akan belajar bagaimana mengira dan bekerja dengan derivatif. Derivatif pertama memberi anda maklumat berdasarkan kecerunan garis tangen ke persamaan. Contohnya, derivatif memberitahu anda kadar perubahan sesuatu dalam situasi tidak linear. Derivatif kedua akan memberitahu anda sama ada fungsi itu meningkat atau menurun pada selang waktu tertentu sehingga anda dapat menentukan kesimpulan fungsi.
- Integral akan mengajar anda cara mengira luas di bawah lengkung dan juga isipadu.
- Kalkulus di sekolah menengah biasanya berakhir dengan urutan dan urutan. Walaupun pelajar tidak akan melihat banyak aplikasi untuk litar, litar penting bagi mereka yang mempelajari persamaan pembezaan.
Bahagian 3 dari 6: Asas Matematik - Penambahan Sarjana

Langkah 1. Mulakan dengan fakta "+1"
Menambah 1 ke nombor membawa anda ke nombor tertinggi di garis nombor. Contohnya, 2 + 1 = 3.
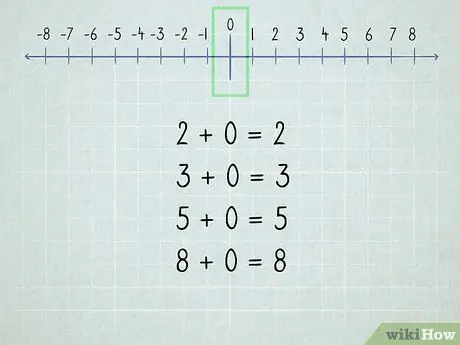
Langkah 2. Memahami sifar
Semua nombor yang ditambahkan ke sifar adalah nombor yang sama kerana "sifar" bermaksud "tidak ada."

Langkah 3. Belajar nombor dua
Pelbagai nombor adalah masalah yang melibatkan penambahan dua nombor sama. Contohnya, 3 + 3 = 6 adalah contoh persamaan yang melibatkan beberapa nombor.

Langkah 4. Gunakan pemetaan untuk mengetahui mengenai penyelesaian penambahan lain
Dalam contoh di bawah, anda belajar dengan memetakan apa yang berlaku apabila anda menambahkan 3 hingga 5, 2 dan 1. Cuba sendiri masalah "tambah dengan 2".

Langkah 5. Teruskan sehingga jumlahnya melebihi 10
Belajar untuk menambah 3 nombor untuk mendapatkan nombor yang lebih besar daripada 10.
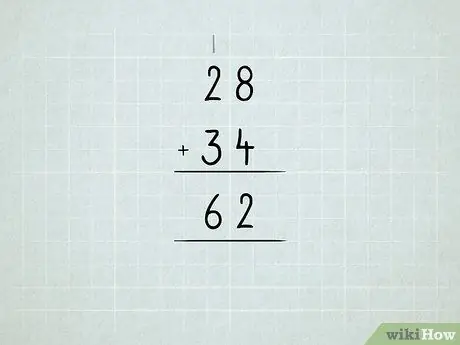
Langkah 6. Tambahkan nombor yang lebih besar
Ketahui mengenai penyatuan semula unit menjadi puluhan, puluhan hingga ratusan, dan sebagainya.
- Tambahkan nombor di lajur kanan terlebih dahulu. 8 + 4 = 12, yang bermaksud anda mempunyai 1 nombor 10 dan 2 nombor 1. Tuliskan nombor 2 di bawah lajur unit.
-
Tulis nombor 1 di lajur puluhan.
-
Tambahkan lajur puluhan secara keseluruhan.
Bahagian 4 dari 6: Asas Matematik - Strategi Pengurangan

Langkah 1. Mulakan dengan "digit 1 ke belakang
Menolak 1 dari nombor membawa anda kembali 1 nombor. Contohnya, 4 - 1 = 3.

Langkah 2. Belajar tolak nombor dua
Contohnya, anda menambah nombor 5 + 5 untuk mendapatkan 10. Cukup tulis persamaan ke belakang untuk mendapatkan 10 - 5 = 5.
- Sekiranya 5 + 5 = 10, maka 10 - 5 = 5.
-
Sekiranya 2 + 2 = 4, maka 4 - 2 = 2.

Langkah 3. Menghafal keluarga fakta
Sebagai contoh:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Langkah 4. Cari nombor yang hilang
Contohnya, _ + 1 = 6 (jawapannya adalah 5).

Langkah 5. Ingat fakta penolakan hingga 20

Langkah 6. Berlatih mengurangkan nombor 1 digit dari nombor 2 digit tanpa meminjam
Kurangkan nombor di lajur satu dan kurangkan nombor di lajur puluhan.
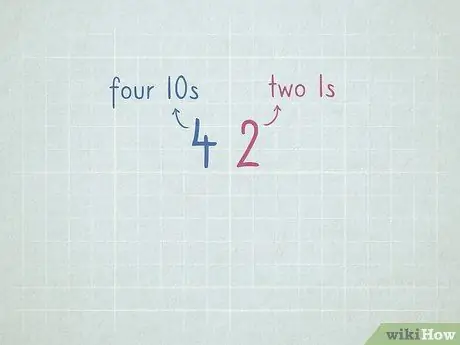
Langkah 7. Amalkan nilai tempat untuk mempersiapkan pengurangan dengan meminjam
- 32 = 3 nombor 10 dan 2 nombor 1.
- 64 = 6 nombor 10 dan 4 nombor 1.
- 96 = _ nombor 10 dan _ nombor 1.
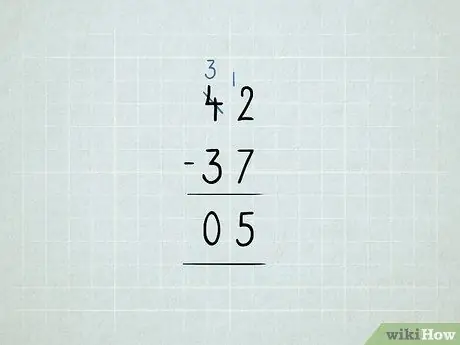
Langkah 8. Kurangkan dengan meminjam
- Anda mahu tolak 42 - 37. Anda mulakan dengan mencuba mengurangkan 2 - 7 di lajur unit. Ternyata, ia tidak berjaya!
-
Pinjam nombor 10 dari lajur puluhan dan letakkan di lajur yang satu. Sekarang anda mempunyai 3 10 bukannya 4 10. Sekarang anda mempunyai 12 1 bukannya 2 1.
-
Kurangkan lajur unit anda terlebih dahulu: 12 - 7 = 5. Kemudian, periksa lajur puluhan. Oleh kerana 3 - 3 = 0, anda tidak perlu menuliskan nombor 0. Jawapan anda ialah 5.
Bahagian 5 daripada 6: Asas Matematik - Pendaraban Master

Langkah 1. Mulakan dengan nombor 1 dan nombor 0
Semua nombor yang didarabkan dengan 1 adalah sama dengan nombor itu sendiri. Sebilangan nombor yang didarabkan dengan 0 sama dengan sifar.

Langkah 2. Menghafal jadual pendaraban

Langkah 3. Berlatih dengan masalah pendaraban satu digit

Langkah 4. Darabkan nombor 2 digit dengan nombor 1 digit
- Darabkan nombor kanan bawah dengan nombor kanan atas.
-
Gandakan nombor kanan bawah dengan nombor kiri atas.
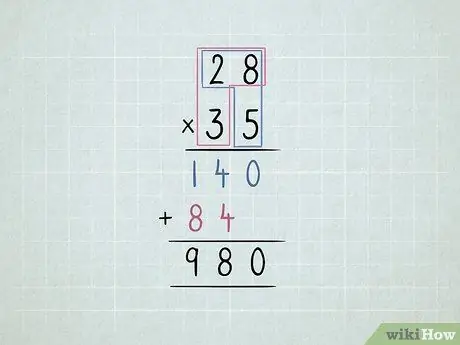
Langkah 5. Darabkan 2 nombor 2 digit
- Gandakan nombor kanan bawah dengan nombor kanan atas dan kemudian dengan nombor kiri atas.
-
Gerakkan baris kedua satu digit ke kiri.
- Gandakan nombor kiri bawah dengan nombor kanan atas dan kemudian nombor kiri atas.
-
Tambahkan semua lajur.
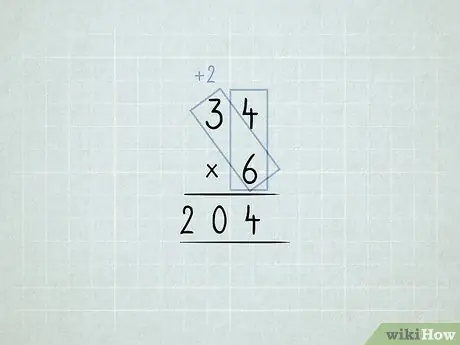
Langkah 6. Gandakan dan kumpulkan semula lajur
- Anda mahu mengalikan 34 x 6. Anda mulakan dengan mengalikan lajur unit (4 x 6), tetapi anda tidak boleh mempunyai 24 1s di lajur yang satu.
-
Simpan 4 1s di ruang unit. Pindahkan 2 10s ke lajur puluhan.
-
Gandakan 6 x 3, yang sama dengan 18. Tambahkan 2 yang anda pindahkan, yang sama dengan 20.
Bahagian 6 dari 6: Asas Matematik - Mengungkap Masalah Pembahagian

Langkah 1. Fikirkan pembahagian berbanding pendaraban
# * Jika 4 x 4 = 16, maka 16/4 = 4.
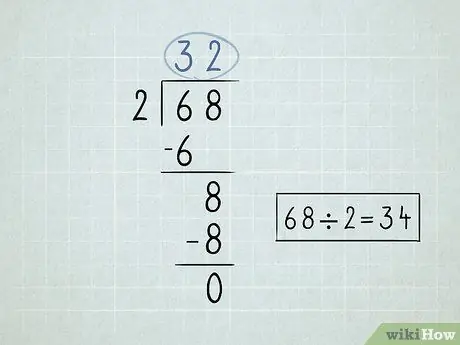
Langkah 2. Tuliskan masalah pembahagian anda
- Bahagikan nombor di sebelah kiri simbol pembahagian, atau pembahagi, dengan nombor pertama di bawah simbol pembahagi. Oleh kerana 6/2 = 3, anda akan menulis nombor 3 di atas simbol pembahagian.
-
Gandakan nombor di atas simbol pembahagian dengan pembahagi. Bawa hasilnya ke bahagian bawah nombor pertama di bawah simbol pembahagian. Oleh kerana 3 x 2 = 6, maka anda akan menurunkan nombor 6 ke bawah.
- Kurangkan 2 nombor yang telah anda tulis. 6 - 6 = 0. Anda boleh meninggalkan 0 kosong, kerana biasanya anda tidak memulakan angka dengan 0.
-
Turunkan nombor kedua yang berada di bawah simbol pembahagian.
- Bahagikan nombor yang anda turunkan oleh pembahagi. Dalam kes ini, 8/2 = 4. Tuliskan nombor 4 di atas simbol pembahagian.
-
Gandakan nombor kanan atas dengan pembahagi dan turunkan nombornya. 4 x 2 = 8.
-
Kurangkan nombor tersebut. Pengurangan terakhir mengembalikan sifar, yang bermaksud anda telah menyelesaikan masalahnya. 68 x 2 = 34.

Langkah 3. Kira juga baki
Sebilangan pembahagi tidak dibahagikan sepenuhnya kepada nombor lain. Sekiranya anda telah menyelesaikan pengurangan terakhir, dan anda tidak mempunyai nombor lagi yang diperoleh, maka nombor terakhir adalah selebihnya.






