- Pengarang Jason Gerald [email protected].
- Public 2024-01-15 08:20.
- Diubah suai terakhir 2025-01-23 12:42.
Anda mungkin berfikir bahawa bilangan bulat hanyalah nombor biasa, seperti 3, -12, 17, 0, 7000, atau -582. Integer juga disebut nombor bulat kerana ia tidak terbahagi kepada bahagian seperti pecahan dan perpuluhan. Baca artikel ini untuk mengetahui semua yang anda perlukan mengenai penambahan dan pengurangan bilangan bulat, atau baca terus bahagian yang anda perlukan.
Langkah
Kaedah 1 dari 5: Menambah dan Menolak Integer Positif Menggunakan Garis Nombor

Langkah 1. Fahami tentang garis nombor
Garis nombor menjadikan matematik asas menjadi sesuatu yang nyata dan fizikal yang dapat anda lihat. Dengan hanya beberapa tanda dan akal sehat, kita dapat menggunakannya seperti kalkulator untuk menambah dan mengurangkan nombor.

Langkah 2. Lukiskan garis nombor asas
Bayangkan atau lukiskan garis lurus yang sama rata. Buat titik di tengah garisan anda. Tulis 0 atau sifar selepas tempoh ini.
Buku matematik anda mungkin menyebutnya sebagai titik permulaan kerana ia adalah titik permulaan bagi semua nombor

Langkah 3. Lukis dua titik, masing-masing di sebelah kanan dan kiri sifar anda
Tulis - 1 di sebelah titik di sebelah kiri dan
Langkah 1. di sebelah titik di sebelah kanan. Ini adalah bilangan bulat yang paling hampir dengan sifar.
- Jangan bimbang untuk membuat jarak antara titik-titik yang sama - selagi anda tahu maksud setiap titik, garis nombor boleh digunakan.
- Bahagian kiri adalah permulaan ayat.

Langkah 4. Lengkapkan garis nombor anda dengan menambahkan lebih banyak nombor
Buat titik lebih banyak ke kiri daripada -1 dan ke kanan daripada 1. Di sebelah kiri, dari -1, tandakan titik anda dengan - 2, - 3, dan - 4. Di sebelah kanan, dari 1, tandakan titik anda dengan
Langkah 2
Langkah 3., da
Langkah 4.. Anda boleh meneruskan sekiranya terdapat ruang di kertas anda.
Contoh dalam rajah menunjukkan garis nombor dari -6 hingga 6

Langkah 5. Memahami tentang bilangan bulat positif dan negatif
Bilangan bulat positif, juga disebut nombor semula jadi, adalah bilangan bulat yang lebih besar daripada sifar. 1, 2, 3, 25, 99, dan 2007 adalah bilangan bulat positif. Bilangan bulat negatif adalah bilangan bulat yang kurang dari sifar (seperti -2, -4, dan -88).
Bilangan bulat adalah kaedah lain untuk memanggil nombor bulat. Pecahan seperti 1/2 (separuh) hanya sebahagian daripada nombor, jadi mereka bukan bilangan bulat. Sama seperti perpuluhan, misalnya 0.25 (titik sifar dua lima); perpuluhan bukan nombor bulat

Langkah 6. Mula menyelesaikan 1 + 2 dengan meletakkan jari anda pada titik 1
Kami akan menyelesaikan masalah penambahan sederhana 1+2 menggunakan garis nombor yang baru anda buat. Nombor pertama ialah
Langkah 1., jadi mulailah meletakkan jari anda pada nombor tersebut.
-
Adakah soalan ini terlalu mudah?
Sekiranya anda pernah menambahkan, anda mungkin tahu jawapan untuk 1 + 2. Bagus: jika anda mengetahui hasilnya, akan lebih mudah untuk memahami bagaimana garis nombor berfungsi. Kemudian, anda boleh menggunakan garis nombor untuk menyelesaikan masalah penambahan yang lebih sukar atau mempersiapkan matematik yang lebih sukar seperti aljabar.

Langkah 7. Tambah 1 + 2 dengan menggerakkan jari anda 2 titik ke kanan
Luncurkan jari anda ke kanan, hitung bilangan titik (nombor lain) yang anda lalui. Sekiranya anda melepasi 2 mata baru, berhenti. Nombor yang ditunjukkan jari anda adalah jawapannya,
Langkah 3
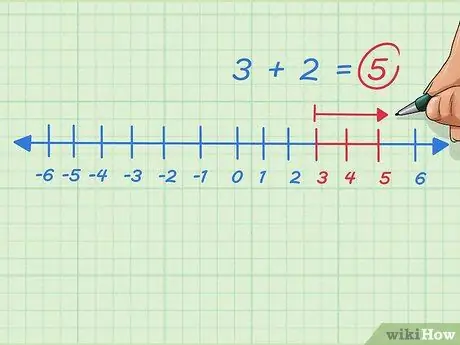
Langkah 8. Tambahkan sebarang bilangan bulat positif dengan bergerak ke kanan pada garis nombor
Katakan kita mahu menyelesaikan 3 + 2. Mulakan pukul 3, bergerak ke kanan atau tambah 2 titik. Kami berhenti pada pukul 5. Masalahnya ditulis 3 + 2 = 5.

Langkah 9. Kurangkan bilangan bulat positif dengan bergerak ke kiri pada garis nombor
Sebagai contoh, kita mahu menyelesaikan 6 -4, kita bermula pada 6, bergerak ke kiri 4 mata, dan berhenti pada 2. Masalah ini ditulis 6 - 4 = 2.
Kaedah 2 dari 5: Menambah dan Menolak Nombor Negatif Menggunakan Garis Nombor

Langkah 1. Ketahui mengenai garis nombor
Sekiranya anda tidak tahu bagaimana membuat garis nombor, kembali ke bahagian Menambah dan Menolak Nombor Positif Menggunakan Garis Nombor untuk mempelajari cara membuatnya.
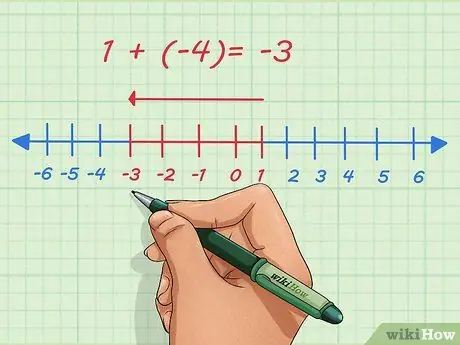
Langkah 2. Memahami tentang nombor negatif
Nombor positif ditunjukkan oleh arah ke kanan pada garis nombor. Nombor negatif ditunjukkan di sebelah kiri pada garis nombor. Menambah nombor negatif bermaksud menggerakkan titik ke kiri pada garis nombor.
-
Sebagai contoh, mari tambah 1 dan -4. Biasanya, soalan ini ditulis seperti ini:
1 + (-4)
. Pada garis nombor, kita bermula di 1, bergerak 4 mata ke kiri dan berhenti di -3.
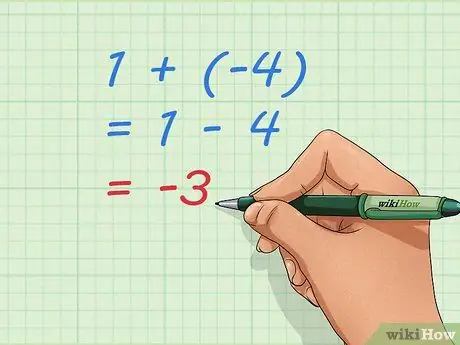
Langkah 3. Gunakan persamaan asas untuk memahami penambahan nombor negatif
Perhatikan bahawa -3, jawapan kita, adalah nombor yang akan kita peroleh jika kita melakukan 1 - 4. Menambah 1 + (-4) dan mengurangkan 4 dari 1 adalah masalah yang sama. Kita boleh menulisnya sebagai persamaan, ayat matematik yang menunjukkan persamaan: 1 + (-4) = 1 - 4 = -3
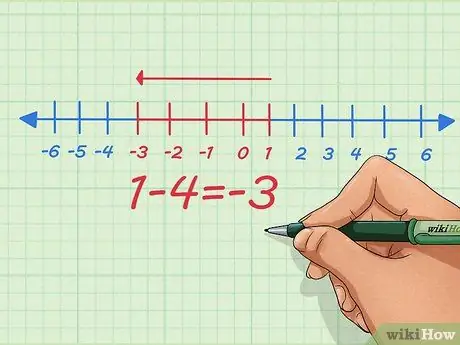
Langkah 4. Daripada menambah nombor negatif, ubah menjadi masalah pengurangan menggunakan nombor positif
Seperti yang dapat kita lihat dari persamaan mudah di atas, kita dapat melakukan kedua - mengubah penambahan nombor negatif menjadi pengurangan nombor positif dan sebaliknya. Anda mungkin telah diajar untuk mengubah negatif menjadi negatif tanpa mengetahui sebabnya - inilah sebabnya.
-
Contohnya, -4. Apabila kita menambah -4 dan 1, kita tolak 1 hingga 4. Ia boleh ditulis dalam matematik dengan menulis
1 + (-4) = 1 - 4
. Kita boleh menuliskannya pada garis nombor, bermula dari titik permulaan pada 1, kemudian menambah 4 titik di sebelah kiri (dengan kata lain, menambah -4). Oleh kerana ini adalah persamaan, satu perkara sama dengan yang lain - jadi sebaliknya juga berlaku
1 - 4 = 1 + (-4)
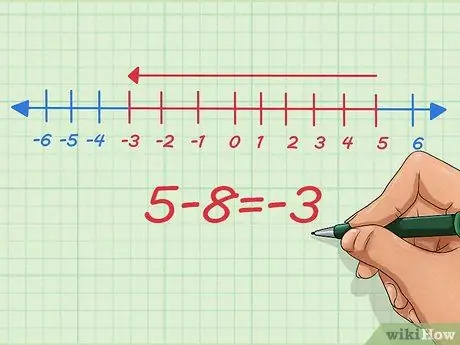
Langkah 5. Fahami cara mengurangkan nombor negatif pada garis nombor
Pada garis nombor, tolak nombor negatif adalah sama dengan mengurangkan panjang. Mari mulakan dengan 5 - 8.
Pada garis nombor, kita bermula di titik permulaan pada 5, tolak 8, dan berhenti di -3
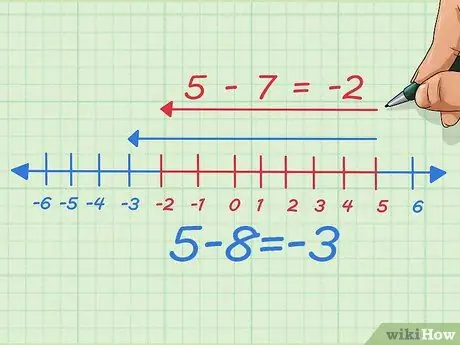
Langkah 6. Kurangkan jumlah yang anda tolak dan lihat apa yang berlaku
Katakan kita tolak satu, nombor yang kita tolak, atau dengan kata lain tolak 7 dan bukan 8. Sekarang kita tolak satu titik ke kiri pada garis nombor. Secara bertulis, kami bermula dengan 5 - 8 = -3 Sekarang, kami hanya bergerak 7 ke kiri, jadi ia menjadi 5 - 7 = -2
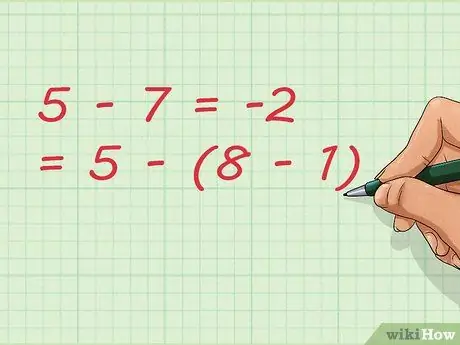
Langkah 7. Perhatikan bahawa penolakan boleh berlaku sebagai tambahan
Dalam contoh kita, kita mengurangkan nombor 1. Dalam menulis persamaan, kita dapat menulisnya lebih pendek seperti: 5 - 7 = -2 = 5 - (8 - 1)

Langkah 8. Tukarkan tanda negatif menjadi positif semasa menambahkan nombor negatif
Dengan menggunakan langkah menukar semua pengurangan kepada penambahan, kita dapat menulis yang lebih pendek seperti: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Kami sudah mengetahui bahawa 5 - 8 = -3, jadi keluarkan 5 - 8 dari persamaan dan masukkan -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Kita sudah tahu bahawa 5 - (8 - 1) - tolak satu titik dari 5 - 8. Persamaan kita dapat menunjukkan bahawa 5 - 8 sama dengan -3, dan tolak satu titik memberi -2. Persamaan boleh ditulis seperti ini:
-3 - (-1) = -3 + 1
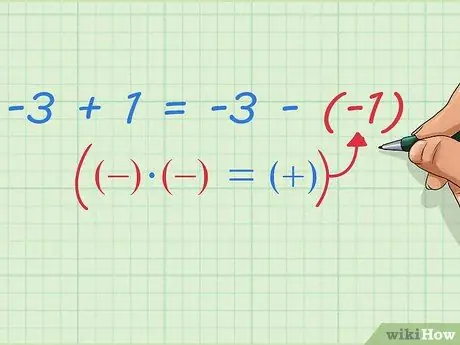
Langkah 9. Tulis penolakan nombor negatif sebagai penambahan
Perhatikan apa yang berlaku selepas ini - kita sudah membuktikan bahawa: -3 + 1 = -3 - (-1) Kita dapat menulis ini dengan peraturan penulisan matematik yang lebih mudah dan umum: nombor pertama ditambah nombor kedua = nombor pertama tolak (nombor kedua negatif) Atau, cara yang lebih mudah yang mungkin anda dengar di kelas matematik: Ubah dua tanda negatif menjadi tanda positif.
Kaedah 3 dari 5: Menambah Integer Besar Positif

Langkah 1. Tuliskan masalah penambahan 2,503 + 7,461 dengan satu nombor berbanding yang lain
Tuliskan nombor di lajur besar sehingga 2 melebihi 7, 5 lebih dari 4, dan seterusnya. Dengan cara ini, kita akan belajar bagaimana menambahkan bilangan bulat yang terlalu besar untuk membayangkan atau menggunakan garis nombor.
Tulis tanda + di sebelah kiri nombor di bawah dan garis di bawahnya, kerana anda mungkin mengetahui masalah penambahan yang lebih kecil
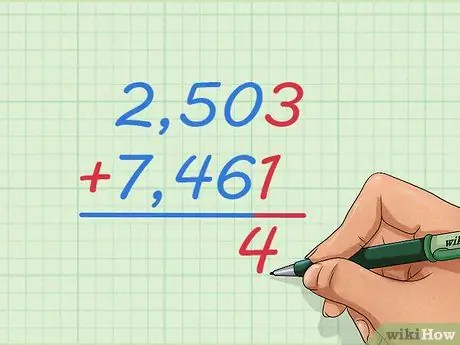
Langkah 2. Mulakan dengan menambahkan dua nombor di sebelah kanan
Mungkin agak pelik untuk bermula dari kanan kerana kita membaca nombor dari kiri. Kita harus menambah dari kanan untuk mendapatkan jawapan yang betul, yang dapat anda lihat kemudian.
-
Di bawah dua nombor paling kanan,
Langkah 3. da
Langkah 1., tuliskan jumlah kedua-duanya
Langkah 4..

Langkah 3. Tambahkan setiap nombor di lajur dengan cara yang sama
Bergerak ke kiri, tambah 0+6, 5+4, dan 2+7. Tulis jawapan di bawah setiap pasangan nombor.
Jawapan anda mestilah: 9.964. Periksa kerja anda jika anda melakukan kesalahan.

Langkah 4. Sekarang tambah 857 + 135
Anda akan melihat sesuatu yang berbeza sebaik sahaja anda menambah pasangan nombor pertama di sebelah kanan. 7+5 sama dengan 12, nombor dua digit, tetapi anda hanya boleh menulis satu digit di bawah lajur itu. Teruskan membaca untuk mengetahui apa yang harus anda lakukan dan mengapa anda harus selalu bermula dari kanan dan bukan dari kiri.

Langkah 5. Tambah 7 + 5 dan ketahui di mana untuk menulis jawapannya
7 + 5 = 12, tetapi anda tidak boleh meletakkan 1 dan 2 di bawah garis. Tetapi, tuliskan digit terakhir, Langkah 2., di bawah garis dan tuliskan digit pertama
Langkah 1., di atas lajur di sebelah kiri, 5 + 3.
-
Sekiranya anda ingin tahu bagaimana ia berfungsi, fikirkan apa maksud pemisahan 1 dan 2. Anda sebenarnya membahagi 12
Langkah 10. da
Langkah 2.. Anda boleh menulis 10 di atas nombor jika anda mahu, dan anda akan melihat 1 di lajur 5 dan 3, seperti sebelumnya.

Langkah 6. Tambahkan 1 + 5 + 3 untuk mendapatkan digit jawapan seterusnya
Kini anda mempunyai tiga digit untuk ditambahkan kerana anda menambahkan 1 pada lajur ini. Jawapannya ialah
Langkah 9., jadi jawapan anda menjadi 92.
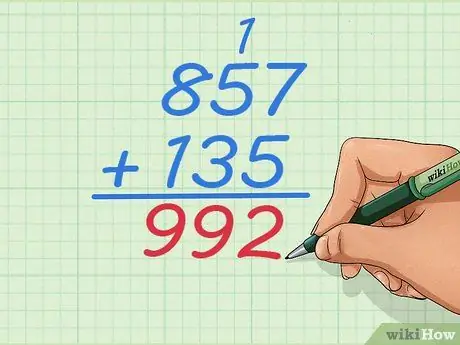
Langkah 7. Selesaikan masalah seperti biasa
Terus buat digit di sebelah kiri sehingga anda menambah semua nombor, dalam kes ini, hanya tinggal satu lajur. Jawapan terakhir anda adalah 992.
- Anda boleh mencuba soalan yang lebih rumit, seperti 974 + 568. Ingatlah, setiap kali anda mendapat nombor dua digit, tuliskan digit terakhir sebagai jawapan dan letakkan digit lain di atas lajur di sebelah kiri, yang akan anda tambah seterusnya. Sekiranya jawapan di lajur terakhir (paling kiri) mengandungi dua digit, tuliskan sebagai jawapan anda.
- Lihat bahagian Petua untuk jawapan kepada soalan 974 + 568 setelah anda berjaya menyelesaikannya.
Kaedah 4 dari 5: Menolak Integer Besar Positif

Langkah 1. Tulis masalah tolak 4.713 - 502 dengan nombor pertama di atas nombor kedua
Tuliskan supaya 3 berada tepat di atas 2, 1 berada di atas 0, 7 di atas 5, dan 4 di atas tempat kosong.
Anda boleh menulis 0 di bawah 4 jika ini membantu anda mengingat nombor mana di atas nombor mana. Anda sentiasa boleh menambah 0 di hadapan nombor tanpa mengubahnya. Pastikan untuk menambahkannya sebelum nombor, bukan selepasnya

Langkah 2. Kurangkan setiap nombor di bawah dari nombor yang betul-betul di atasnya
Sentiasa bermula dari kanan. Selesaikan 3-2, 1-0, 7-5, dan 4-0, tulis jawapan untuk setiap soalan tepat di bawah dua nombor yang dikurangkan.
Hasilnya adalah, 4.211.

Langkah 3. Sekarang tulis soalan 924 - 518 dengan cara yang sama
Nombor ini mempunyai bilangan digit yang sama, jadi anda boleh menuliskannya dengan mudah. Masalah ini akan mengajar anda sesuatu mengenai pengurangan bilangan bulat jika anda belum mengetahuinya.

Langkah 4. Ketahui cara menyelesaikan masalah pertama, yang paling kanan
4 - 8. Masalah ini rumit kerana 4 kurang dari 8, tetapi jangan gunakan nombor negatif, tetapi ikuti langkah berikut:
- Di baris atas, silang 2 dan tulis 1. 2 hendaklah di sebelah kiri 4.
- Salib 4 dan tulis 14. Lakukan ini di ruang yang sempit sehingga jelas bahawa 14 lebih dari 8. Anda juga boleh menulis 1 di depan 4 untuk membuat 14 jika terdapat cukup ruang.
- Yang baru anda lakukan ialah meminjam 1 dari tempat berpuluh atau lajur kedua dari kanan dan menukarnya menjadi 10 di tempat satu atau lajur paling kanan. Apabila nombor 10 sama dengan sepuluh kali ganda nombor 1, maka ia sama.

Langkah 5. Sekarang selesaikan masalah 14 - 8 dan tulis jawapan di bawah lajur paling kanan
Seharusnya ditulis 6 di baris jawapan paling kanan.

Langkah 6. Lengkapkan lajur seterusnya di sebelah kiri, menggunakan nombor baru yang anda tulis
Pengurangan hendaklah 1 - 1, yang sama dengan 0.
Jawapan anda sekarang semestinya 06.

Langkah 7. Selesaikan masalah dengan menyelesaikan pengurangan terakhir, lajur paling kiri
9 - 5 = 4, jadi jawapan terakhir anda adalah 406.

Langkah 8. Sekarang kita menyelesaikan masalah mengurangkan nombor besar dari bilangan kecil
Katakan anda diminta untuk melengkapkan 415,990 - 968,772. Tulis nombor kedua di bawah nombor pertama dan anda akan menyedari bahawa nombor di bawah lebih besar! Anda dapat mengetahui dengan segera dari digit pertama di sebelah kiri: 9 lebih besar daripada 4, jadi angka yang bermula dengan 9 lebih besar.
Pastikan anda menulis lajur dengan betul sebelum membandingkan. 912 tidak lebih besar daripada 5000 anda dapat mengetahui jika anda menulis lajur dengan betul kerana tidak ada nombor di bawah 5. Anda boleh menambahkan pertolongan sifar, misalnya, tulis 912 dengan 0912 sehingga lajur sama dengan 5000.

Langkah 9. Tulis nombor yang lebih kecil di bawah nombor yang lebih besar dan tambahkan tanda - di hadapan jawapan
Setiap kali anda mengurangkan nombor dari nombor yang lebih kecil, hasilnya adalah nombor negatif. Lebih baik menulis tanda ini sebelum mengurangkan supaya anda tidak lupa menuliskannya.

Langkah 10. Untuk menjawab, tolak nombor kecil dari nombor besar dan ingat untuk menulis tanda -
Jawapan anda akan menjadi negatif, yang ditunjukkan dengan tanda -. Jangan cuba mengurangkan sebilangan besar dari sebilangan kecil, kemudian menjadikan hasilnya negatif; jawapan anda akan salah.
Masalah baru yang harus diselesaikan adalah: 968,772 - 415,990 = -? Lihat bahagian Petua untuk jawapannya setelah berusaha menyelesaikan masalah ini
Kaedah 5 dari 5: Menambah dan Menolak Integer Negatif
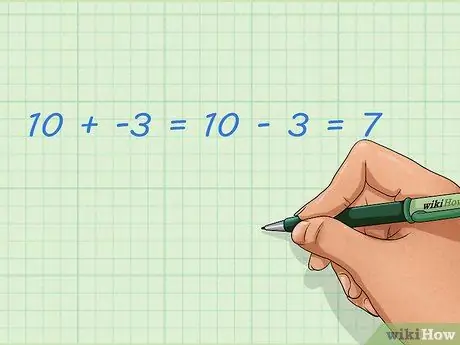
Langkah 1. Ketahui cara menambah nombor negatif dan positif
Menambah bilangan bulat negatif adalah sama dengan mengurangkan bilangan bulat positif. Ini lebih mudah dilakukan dengan garis nombor yang dijelaskan di bahagian lain, tetapi anda juga boleh memikirkannya dengan kata-kata. Nombor negatif bukan nombor biasa; jumlah ini kurang daripada sifar dan boleh mewakili jumlah yang diambil. Sekiranya anda menambahkan angka ini ke nombor biasa, hasilnya menjadi lebih kecil.
- Contoh: 10 + -3 = 10 - 3 = 7
- Contoh: -12 + 18 = 18 + -12 = 18 - 12 = 6. Ingatlah bahawa anda sentiasa boleh mengubah urutan nombor sebagai tambahan, tetapi tidak dalam pengurangan.
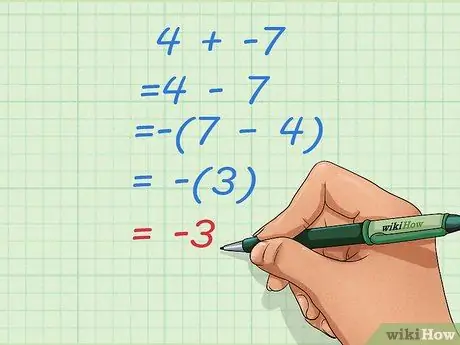
Langkah 2. Ketahui apa yang harus anda lakukan jika mengubahnya menjadi masalah pengurangan dengan bilangan permulaan yang lebih kecil
Kadang kala, menukar penambahan kepada masalah pengurangan seperti yang di atas boleh menyebabkan jawapan ganjil seperti 4 - 7. Apabila ini berlaku, ubah urutan nombor dan buat hasil anda negatif.
- Katakan masalah awal anda ialah 4 + -7.
- Ubah menjadi masalah pengurangan: 4 - 7
- Balikkan urutan dan buat hasilnya negatif: - (7 - 4) = - (3) = -3.
- Sekiranya anda tidak biasa menggunakan tanda kurung dalam persamaan, fikirkan perkara ini: 4 - 7 berubah menjadi 7 - 4 dengan penambahan tanda negatif. 7 - 4 = 3, tetapi kita harus mengubahnya menjadi -3 supaya jawapan kepada soalan 4 - 7 betul.
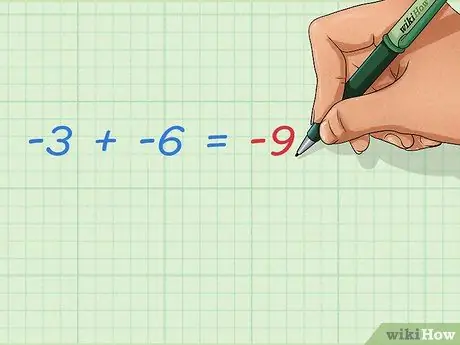
Langkah 3. Ketahui cara menambahkan dua bilangan bulat negatif
Dua nombor negatif yang ditambahkan selalu menjadikan hasil negatif lebih besar. Oleh kerana tidak ada nombor positif yang ditambahkan, hasilnya akan jauh dari 0. Jawapannya mudah:
- -3 + -6 = -9
- -15 + -5 = -20
- Adakah anda melihat coraknya? Yang harus anda lakukan ialah menambahkan nombor seolah-olah itu nombor positif dan menambahkan tanda negatif. -4 + -3 = - (4 + 3) = -7
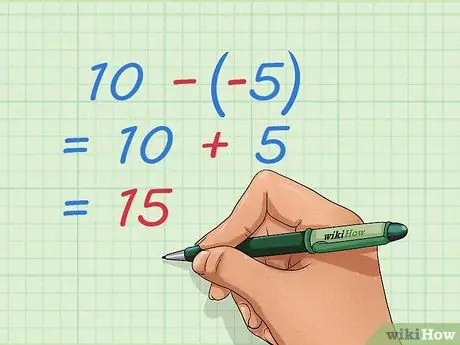
Langkah 4. Ketahui cara mengurangkan bilangan bulat negatif
Seperti masalah penambahan, anda boleh menulis semula masalahnya sehingga anda hanya mempunyai nombor positif. Sekiranya anda mengurangkan nombor negatif, anda akan membuang beberapa perkara yang telah diambil, yang sama dengan menambahkan nombor positif.
- Fikirkan nombor negatif sebagai wang yang dicuri. Sekiranya anda mengurangkan atau mengambil wang yang dicuri sehingga anda dapat mengembalikannya, seperti memberi wang kepada seseorang, bukan?
- Contoh: 10 - -5 = 10 + 5 = 15
- Contoh: -1 - -2 = -1 + 2. Anda sudah belajar bagaimana menyelesaikan masalah ini pada langkah pertama, ingat? Baca semula cara menambah nombor negatif dan positif jika anda terlupa.
- Inilah penyelesaian lengkap contoh terakhir: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Petua
- Anda mungkin telah menulis nombor panjang seperti 2,521,301 menggunakan koma (,) dan bukan (.) Bergantung pada tempat anda tinggal. Gunakan apa yang diminta oleh guru anda agar anda tidak keliru dengan sistem tulisan yang lain.
- Lukiskan garis nombor anda pada skala yang berbeza untuk mewakili nombor yang berbeza. Tidak ada peraturan bahawa setiap jarak pada garis nombor sama dengan 1. Bayangkan garis nombor yang 10 bukannya 1. Selain dari fakta bahawa setiap titik 10 sekarang, penambahan dan pengurangan tetap sama. Cubalah jika anda tidak mempercayainya.
- Sekiranya anda mencuba soalan cabaran khas di bahagian Nombor Panjang, berikut jawapannya: 974 + 568 = 1.542. Jawapan dari 415,990 - 968,772 adalah - 552.782.






