Selagi anda mengetahui ukuran dua sudut yang lain, mencari sudut ketiga segitiga adalah mudah. Anda hanya perlu mengurangkan jumlah dua sudut sebanyak 180 darjah. Namun, ada juga cara lain yang boleh anda gunakan untuk mencari sudut ketiga segitiga jika bentuk masalahnya sedikit berbeza dari biasanya. Sekiranya anda ingin mengetahui cara mencari sudut ketiga segitiga, ikuti panduan di bawah.
Langkah
Kaedah 1 dari 3: Menggunakan Ukuran Dua Sudut Lain
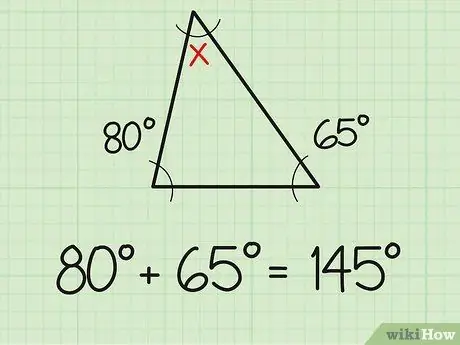
Langkah 1. Tambah dua sudut yang diketahui
Satu fakta yang harus anda ketahui ialah jumlah tiga sudut segitiga selalu 180 darjah. Oleh itu, jika anda sudah mengetahui ukuran dua sudut segitiga, mencari sudut ketiga akan semudah melakukan masalah penambahan dan pengurangan yang mudah. Pertama, tambahkan dua ukuran sudut yang sudah anda ketahui. Contohnya, dua sudut yang diketahui berukuran 80 dan 65 darjah. Tambah keduanya (80 + 65), dan anda mendapat 145 darjah.
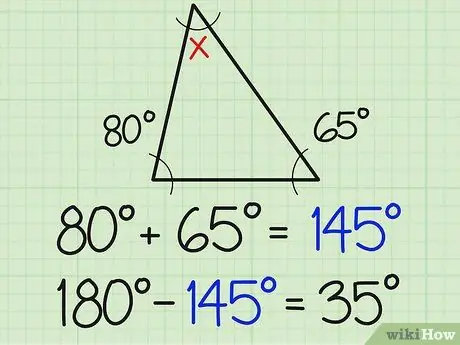
Langkah 2. Bahagikan nombor itu dengan 180
Jumlah tiga sudut segitiga selalu 180 darjah. Oleh itu, sudut ketiga mestilah 180 apabila ditambahkan pada jumlah dua ukuran sudut yang diketahui. Dalam contoh di atas, ini bermaksud 180-154 = 35.
Langkah 3. Tulis jawapan anda
Sekarang anda mempunyai jawapan untuk sudut ketiga (dalam contoh 35 darjah). Sekiranya anda masih ragu-ragu, lihat sendiri. Tambahkan tiga sudut bersama-sama, dan anda akan mendapat hasil 180. Sekiranya tidak, pengiraan anda salah. Untuk contoh ini, 80 + 65 + 35 = 180. Sekiranya betul, ini bermakna anda telah menyelesaikan masalahnya.
Kaedah 2 dari 3: Menggunakan Pemboleh ubah
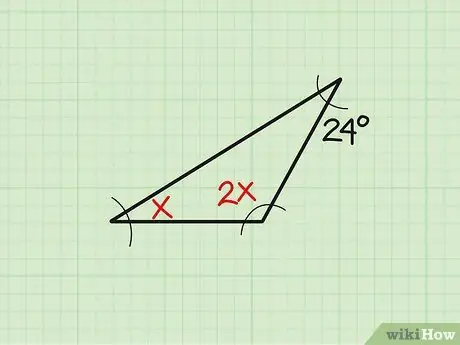
Langkah 1. Tuliskan masalahnya
Kadang-kadang, ukuran sudut yang ada ditunjukkan dalam bentuk berubah-ubah. Mari kita ambil contoh ini: "Cari sudut" x "segitiga jika tiga sudut masing-masing mengukur" x "," 2x ", dan 24." Pertama, tuliskan masalahnya.
Langkah 2. Tambahkan semua ukuran sudut
Prinsip yang mesti anda ingat tetap sama. Jadi, tambahkan dahulu tiga sudut dalam masalah tersebut, iaitu "x + 2x + 24 = 3x + 24".
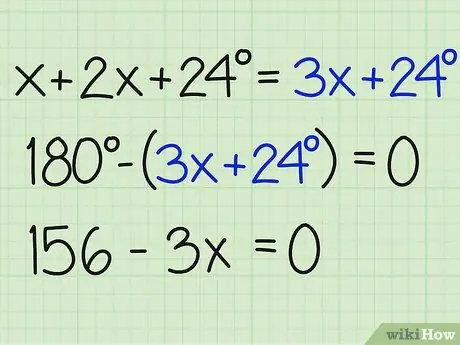
Langkah 3. Bahagikan jumlah sudut dengan 180
Sekarang, bezakan nombor itu dengan 180 darjah untuk mencari x dan cari jawapan untuk masalah itu. Pastikan anda mengakhiri persamaan dengan sifar. Inilah cara penulisannya:
- 180- (3x + 24) = 0
- 180-3x-24 = 0
- 156-3x = 0
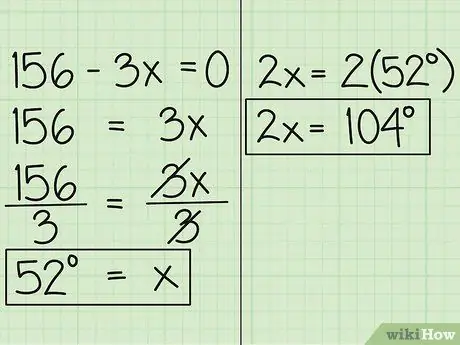
Langkah 4. Cari nilai x
Sekarang, pindahkan pemboleh ubah ke sisi lain dari persamaan, dan anda akan mendapat 156 = 3x. Kemudian, bahagikan persamaan dengan 3, sehingga anda mendapat x = 52. Ini bermaksud bahawa ukuran sudut yang dinyatakan dalam x ialah 52 darjah. Sudut yang lain, dinyatakan dalam 2x adalah 52 darjah kali 2, iaitu 104 darjah.
Langkah 5. Periksa keputusan anda
Sekiranya anda ingin memastikan jawapan anda betul, cukup tambahkan tiga ukuran sudut yang sudah anda dapati jawapannya. Sekiranya hasilnya adalah 180, ini bermakna jawapan anda betul. Untuk contoh ini, 52 + 104 + 24 = 180.
Kaedah 3 dari 3: Menggunakan Kaedah Lain
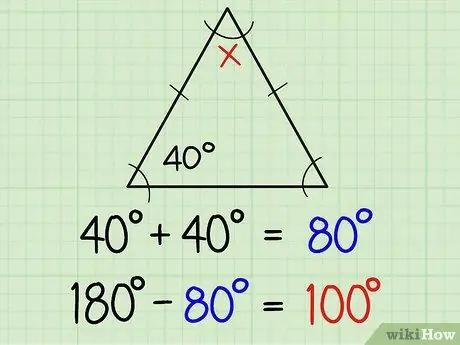
Langkah 1. Cari sudut segitiga isosceles
Segitiga isoskel mempunyai dua sisi yang sama dan dua sudut yang sama. Dua sisi yang sama biasanya ditandai dengan garis kecil di tengah garis sisi, yang bermaksud bahawa dua sudut bertentangan pada garis adalah ukuran yang sama. Sekiranya anda sudah mengetahui ukuran satu sudut, secara automatik anda akan mengetahui sudut yang lain. Berikut penjelasan lebih lanjut:
Sekiranya salah satu sudut sama ialah 40 darjah, maka sudut yang lain ialah 40 darjah. Dengan cara itu anda dapat menemui ketiga-tiga sudut dengan perbezaan antara jumlah 40 + 40 (iaitu 80) dan 180, atau dengan kata lain 180-80 = 100
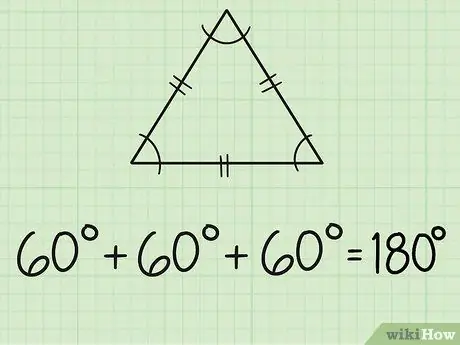
Langkah 2. Cari sudut segitiga sama sisi
Segi tiga sama sisi mempunyai tiga sisi yang sama dan tiga sudut yang sama. Setiap sisi biasanya ditandai dengan dua garis pendek di tengah. Oleh kerana ketiga-tiga sudut adalah sama, ini bermaksud semua sudut mengukur 60 darjah, kerana 180/3 = 60.
Langkah 3. Cari sudut ketiga dalam segi tiga tepat
Katakan anda memperoleh segitiga tepat, dengan salah satu sudut akut berukuran 30 darjah. Oleh kerana segitiga adalah sudut tepat, ini bermaksud bahawa salah satu sudut, iaitu sudut kanan, mesti mengukur 90 darjah. Kemudian gunakan prinsip segitiga, perbezaan antara jumlah dua sudut (90 + 30 = 120) dengan 180, maka anda akan mendapat 180-120 = 60 darjah.
