Dengan pekali korelasi peringkat Spearman kita dapat mengenal pasti sama ada dua pemboleh ubah mempunyai hubungan fungsi monotonik (iaitu, apabila satu nombor meningkat, nombor yang lain juga akan meningkat, atau sebaliknya). Untuk mengira pekali korelasi peringkat Spearman, anda perlu memberi peringkat dan membandingkan set data untuk mencari d2, dan kemudian masukkan data ke dalam formula pekali korelasi peringkat Spearman standard atau dipermudahkan. Anda juga boleh mengira pekali ini menggunakan formula Excel atau perintah R.
Langkah
Kaedah 1 dari 3: Cara manual
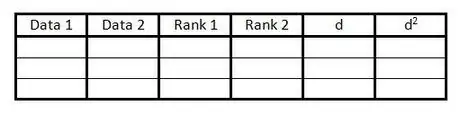
Langkah 1. Buat jadual
Jadual digunakan untuk memasukkan semua maklumat yang diperlukan untuk mengira Pekali Korelasi Spearman Rank. Anda memerlukan jadual seperti ini:
- Buat 6 lajur dengan tajuk, seperti dalam contoh.
- Sediakan sebilangan baris kosong dengan bilangan pasangan data.
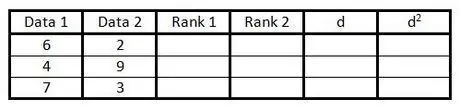
Langkah 2. Isi dua lajur pertama dengan pasangan data
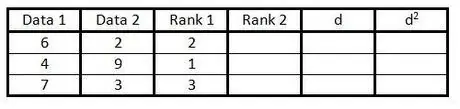
Langkah 3. Masukkan peringkat lajur pertama kumpulan data di lajur ketiga dari 1 hingga n (bilangan data)
Berikan penilaian 1 untuk nilai terendah, penilaian 2 untuk nilai terendah seterusnya, dan seterusnya.
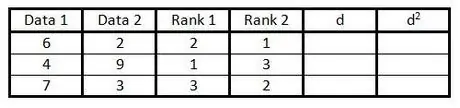
Langkah 4. Pada lajur keempat, lakukan hal yang sama seperti pada langkah 3, tetapi untuk memberi peringkat data di lajur kedua
-
Purata_742 Sekiranya terdapat dua (atau lebih) data yang mempunyai nilai yang sama, hitung nilai purata data, dan kemudian masukkan ke dalam jadual berdasarkan nilai rata-rata ini.
Dalam contoh di sebelah kanan, terdapat dua nilai 5 pada penilaian 2 dan 3. Oleh kerana terdapat dua nilai 5, cari purata penilaian. Purata 2 dan 3 adalah 2.5, jadi masukkan nilai penilaian 2.5 untuk kedua-dua nilai 5.
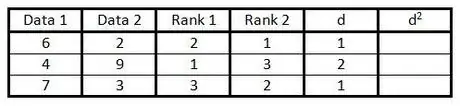
Langkah 5. Di lajur "d" hitung perbezaan antara dua nombor di lajur peringkat
Maksudnya, jika satu lajur berada di peringkat 1 dan lajur yang lain berada di peringkat 3, selisihnya adalah 2. (Tanda itu tidak menjadi masalah, kerana langkah selanjutnya adalah memusatkan nilai.)
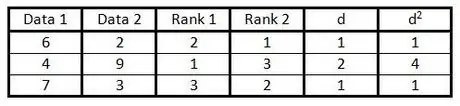
Langkah 6. Segi empat nombor pada lajur "d" dan tuliskan hasilnya di lajur "d2".
Langkah 7. Tambahkan semua data di lajur d2".
Hasilnya adalah d2.
Langkah 8. Pilih salah satu formula berikut:
-
Sekiranya tidak ada penilaian yang sama seperti pada langkah sebelumnya, masukkan nilai ini dalam formula Pekali Korelasi Spearman Rank yang dipermudahkan
Langkah8_271 dan ganti "n" dengan bilangan pasangan data untuk mendapatkan hasilnya.
Langkah9_402 -
Sekiranya terdapat pangkat yang serupa pada langkah sebelumnya, gunakan formula Pekali Korelasi Spearman Rank standard:
Spearman
Langkah 9. Tafsirkan hasilnya
Nilainya boleh berbeza antara -1 dan 1.
- Sekiranya nilainya mendekati -1, korelasi adalah negatif.
- Sekiranya nilainya mendekati 0, tidak ada korelasi linear.
- Sekiranya nilainya hampir dengan 1, korelasi adalah positif.
Kaedah 2 dari 3: Menggunakan Excel
Langkah 1. Buat lajur baru untuk data bersama dengan peringkatnya
Contohnya, jika data anda berada di Lajur A2: A11, gunakan formula "= RANK (A2, A $ 2: A $ 11)", dan salin ke bawah sehingga merangkumi semua lajur dan baris.
Langkah 2. Tukar penilaian yang sama seperti yang dijelaskan dalam langkah 3 dan 4 kaedah 1
Langkah 3. Di sel baru, hitung korelasi antara dua lajur peringkat dengan formula "= CORREL (C2: C11, D2: D11)"
Dalam contoh ini, C dan D merujuk pada lajur di mana kedudukan berada. Sel baru akan diisi dengan Spearman Rank Correlation.
Kaedah 3 dari 3: Menggunakan R
Langkah 1. Pasang program R terlebih dahulu jika anda belum memilikinya
(Lihat
Langkah 2. Simpan data anda dalam bentuk CSV, letakkan data yang anda ingin cari korelasi dalam dua lajur pertama
Kita boleh melakukan ini dengan menggunakan menu "Simpan sebagai".
Langkah 3. Buka R Editor
Sekiranya anda bekerja dari terminal, jalankan R. Sekiranya anda bekerja dari desktop, klik ikon R.
Langkah 4. Taipkan arahan berikut:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") dan tekan Enter.
- pemeran (pangkat (d [, 1]), pangkat (d [, 2]))
Petua
Data mesti terdiri daripada sekurang-kurangnya 5 pasang supaya trend dapat dilihat (jumlah data adalah 3 pasang dalam contoh hanya untuk mempermudah pengiraan.)
Amaran
- Pekali korelasi peringkat Spearman hanya mengenal pasti kekuatan korelasi di mana data naik atau turun secara konsisten. Sekiranya terdapat trend lain dalam data, korelasi peringkat Spearman tidak akan memberikan perwakilan yang tepat.
- Formula ini didasarkan pada anggapan bahawa tidak ada penilaian yang sama. Apabila terdapat pangkat yang sama seperti dalam contoh, kita harus menggunakan definisi ini: pekali korelasi momen pendaraban dengan pangkat.
